Dr. David R Middlebrook observed that circuit analysis methods, such as loop and node analysis, produce ‘high entropy’ expressions that give no insight into how a circuit operates. This can lead to poor designs and the inability to solve design problems. Loop and node analysis work for analyzing the performance of circuits but don’t work for design. Design is the reverse of analysis. Middlebrook's insight was that design begins with the specifications or answers and works backwards to a circuit topology and its component values. Design oriented analysis results in ‘low entropy’ expressions that provide a direct physical interpretation and enough information to clarify how component values affect the results. ‘Low entropy’ expressions allow the designer to work backwards and change circuit elements in order to meet the design specification.
Low entropy expressions are at the heart of design oriented analysis. For a designer, there is no point in doing the analysis otherwise. There are many different approaches to design oriented analysis. One way this can be accomplished is by doing the algebra on the circuit diagram.
Application of Thevenin’s or Norton’s theorem along with voltage or current division is one method of doing algebra on the circuit diagram.
Figure 1 Voltage Divider
Figure 2 Current Divider
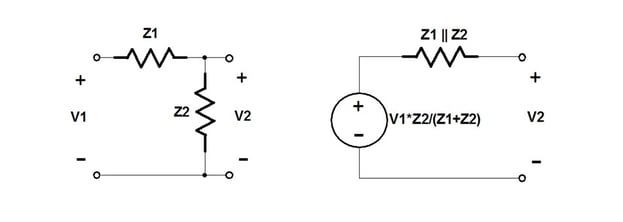
Figure 3 Thevenin's Theorem
Every time Thevenin’s theorem is used one loop is removed from the circuit.
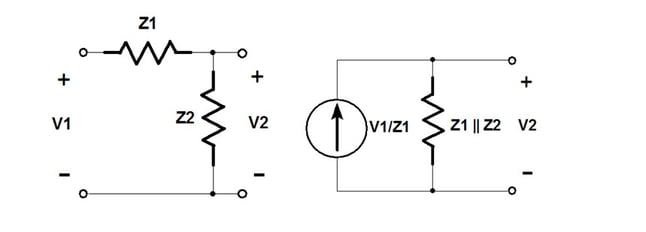
Figure 4 Norton's Theorem
Every time Norton’s theorem is used one node is removed from the circuit.
Figure 5 RC Circuit
As an example, lets create a ‘low entropy’ expression for the voltage transfer function of the circuit in Figure 5. It will be done the hard way, using algebra. First, use voltage division to create a transfer function and then multiply the numerator and denominator by ‘sC’. Next, multiply both the numerator and denominator by ‘1+sCR2’. Finally, use the distributive property to remove R1+R2 from the denominator of transfer function.
The’ low entropy’ result is a low frequency gain and the frequency corner of a pole:
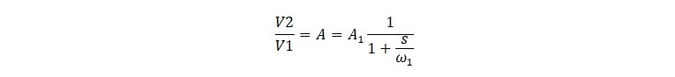
Where,
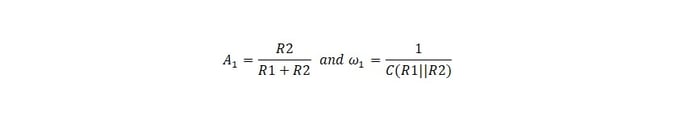
Figure 6 Thevenin Equivalent of the RC Circuit
The easy way is to keep the entropy low from the beginning by using Thevenin’s theorem to eliminate a loop in the circuit as shown in Figure 5. The Thevenin voltage, Vth, is the open circuit voltage across the terminals on either side of R2
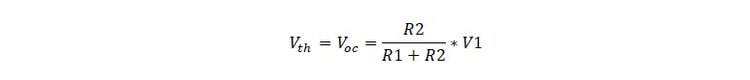
The Thevenin resistance, Rth, is the resistance across the terminals on either side of R2.This would include the 0 Ohm resistance or short circuit of the ideal voltage source. Substituting Vth for the Voltage source and Rth for the R1-R2 voltage divider gives the much simpler circuit of Figure 6.
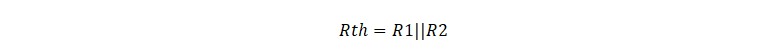
The transfer function can be created by inspection or by using voltage division to create a transfer function and multiplying the numerator and denominator by ‘sC’. This approach takes far less work.
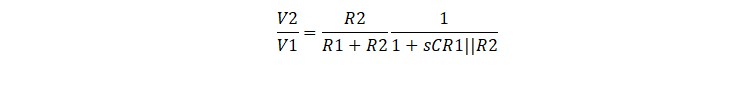Circuit reduction through loop and node removal results in a natural ordering or grouping of circuit elements and terms whose relative importance are readily apparent.
More in depth information on Low Entropy Expressions and Doing the Algebra on the Circuit Diagram can be found in the Venable Vault webpage:
Video Presentation of Technical Therapy for Analog Circuit Designers Part 1 A video lecture and notes are under Chapter 2 - Low Entropy Expressions: The Key to D-OA.
